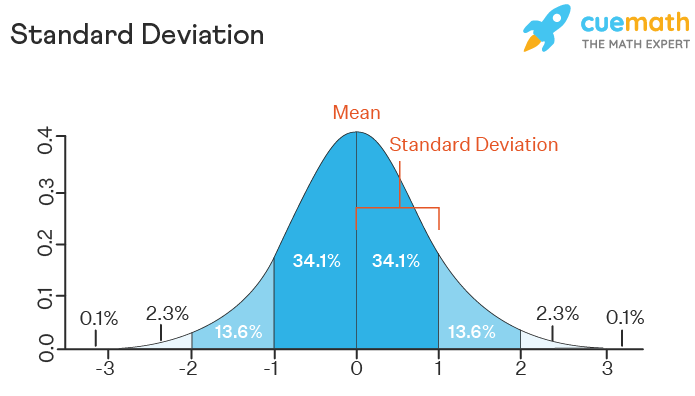
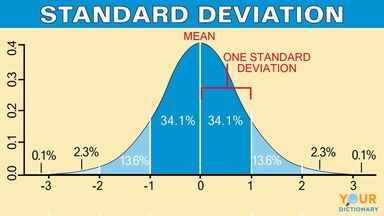
The sample standard deviation is the square root of the sample variance ie As a rough rule of thumb 95 of future data collected should lie between provided and are good estimates for the true population mean and variance and the distribution of the random variable is approximately Normal or Gaussian. The sample standard deviation would tend to be lower than the real standard deviation of the population.
Standard Deviation Formula Definition Methods Examples
Calculate the sample standard deviation and sample variance using the statistical functions on your calculator.
. Standard_deviation_age sdSD_age standard_deviation_age. What is true about inferential statistics. 6 4 2 4.
Compare data from different groups. The sample standard deviation is the square root of the quotient of the sum of the squared deviations from the mean and n. Describe the scores in such a sample.
Key Words measures of spread dispersion range variance standard deviation corrected sum of. In R the syntax for Standard Deviation looks like this. The formula for standard deviation makes use of three variables.
Now the sample standard deviation can be calculated by using the above formula as ơ 1 4 1 4 0 5 1. Describe in your own words why the confidence interval for the mean of five measurements is smaller than that for a single result. In words explain what is measured by each of the following.
From math import sqrt. Mean x 300 430 170 470 600 5 394. N number of values in the sample.
With samples we use n 1 in the formula because using n would give us a biased estimate that consistently underestimates variability. From the formulas above we can see that there is one tiny difference between the population and the sample standard deviation. Methods of Standard Deviation in R.
The squares of the deviations of each variable can be calculated as below 3 4 2 1. Test Score x Difference from the mean x x Difference from the mean x2 Sum of Difference from the mean x x. Work through each of the steps to find the standard deviation.
There are multiple methods to calculate Standard deviation in R. Birds are very good at plotting their migration route the same year after year. Standard Deviation σ.
So the standard deviation of 17 is the square root of the average of the squared differences from. How is Standard Deviation calculated. Calculate the mean of your data set.
Precisely the standard deviation is the square root of the variance which is the average of the squared differences from the mean. 2 4 2 4. Variance σ2 8836 1296 50176 5776 42436 5 21704.
You can convince yourself of this with a simple Series and applying the formulae. Describe the sample standard deviation in words rather than with a formula. If the values instead were a random sample drawn from some larger parent population then we would have divided by 7 which is latextextn-1latex instead of 8 which is latextextnlatex in the denominator of the last formula and then the quantity thus obtained would be called the sample standard deviation.
Sample Mean 4. Standard deviation--average difference between the mean of a sample and each data value in the sample 14 251 Mean of 14 and SD of 251 Distribution Shape. S pdSeries1 2 In 12.
Using words the standard deviation is the square root of the variance of X. Subtract the mean from each of the data values and list the differences. X sample mean.
Suppose youre given the data set 1 2 2 4 6. A SS b Variance c Standard deviation What does it mean for a sample to have a standard deviation of zero. The sample standard deviation is the square root of the quotient of the sum of the squared deviation from the mean and n-1.
Not all random variables have a standard deviation. The standard deviation of 17 shows how much dispersion there is from the mean wage. State whether or not your sample is skewed based on what you know about the patient size mean median and mode.
C Why is Spooled a better estimate of s than the standard deviation from any one sample. A low standard deviation means that the data is very closely related to the average thus very reliable. Describe the spread of your data.
For any set of data at least _______ of the data will be within two standard deviation of the mean. Assess the shape and spread of your data distribution. Be a thorough as possible.
Basically a small standard deviation means that the values in a statistical data set are close to the mean or average of the data set and a large standard deviation means that the values in the data set are farther away from the mean. Calculate the Standard Deviation. Standard deviation square root of what you just calculated variance.
Standard deviation 𝒙𝒙 𝒏 _____. 07071067811865476 and the formula for corrected sample standard deviation. The reason for this is because when we calculate the sample standard deviation.
5 4 2 1. Describe the sample standard deviation in words rather than with a formula. The standard deviation of a probability distribution is the same as that of a random variable having that distribution.
The red line in the graph shows the average height of the dogs. Standard deviation is a statistical measurement of the amount a number varies from the average number in a series. The sample standard deviation.
When calculating the sample standard deviation we divided by n-1 instead of N. For a bell-shaped distribution approximately ______ of the data will be. Describe your sample based on your two factile values 35 th percentile and 3 rd quartile for the PATIENTS variable.
The standard deviation of the Age is 1552926. The first variable is the value of each point within a data set with a sum-number indicating each additional variable x x 1 x 2 x 3 etcThe mean is applied to the values of the variable M and the number of data that is assigned to the variable n. The sample standard deviation is the square root of the quotient of the sum of the squared deviations from the mean and n 1.
Describe what the standard deviation measures for a data set. Describe the center of your data. Its the corrected sample standard deviation.
Describe the size of your sample. The more concentrated the smaller the standard. The standard deviation measures how concentrated the data are around the mean.
The mean of the data is 122465 155 3. Subtract 3 from each of the values 1 2 2 4 6. I would say that this suggests that wages are very spread out.
Birds use the magnetic poles of the earth when migrating each year. A high standard deviation means that there is a large variance between the data and the statistical average and is not as reliable. C Why is Spooled a better estimate of s than the standard deviation from any one sample.
The output of the codes provides us the Standard deviation of the dataset. 4 4 2 0. Include descriptions of your overall sample including sample size mean range and standard deviation.
Examples Of Standard Deviation And How It S Used
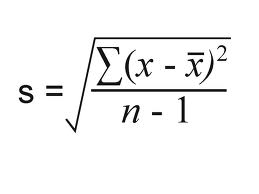
0 Comments